如何制作一款2D平台游戏之触碰测试机制
作者:Paul
本文我将谈论平台游戏背后的技术元素(第1部分请点击这里)。
这里我们采用的语言是actionscript 3.0,但文章所谈论的技巧适合各种语言。
文章中,我将谈及物理原理及碰触测试。
类结构
在这里谈论我在游戏中用于代表移动元素的类结构合情合理:
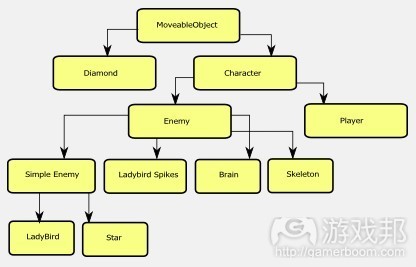
图1所呈现的是类结构——位于顶部的是MoveableObject,这是所有一般触碰测试和回应的操作地点;我这里标明“一般”是因为玩家会进行特殊操作,以应对梯子之类的元素。
结构图中的各层次代表独立功能;例如,Character包含AnimationController,它负责在各角色中呈现不同动画内容。SimpleEnemy代表特定敌人角色,角色和游戏空间没有触碰测试,SimpleEnemy在遇到位置图标时会遵循它们的要求。Diamond属于简单物件,它没有AI,只会和空间碰触,所以它源自基础类,因为这就它所需要的所有功能。
这似乎会给这款简单的游戏带来众多复杂元素,但它其实促使添加新敌人类型变得非常简单,简化故障排除过程,因为各物件共享许多代码。
若要我根据自己的10年开发经验提建议,那就是:不要复制代码。这会带来缓慢的开发过程和众多漏洞问题(游戏邦注:你会在某地点修复内容所存在的漏洞,然后忘记在另一复制地点中进行修复)。
MoveableObject包含若干特性,源自MoveableObject的所有类都得融入这些特性:
* m_HasWorldCollision——是否要进行完整的触碰测试
* m_ApplyGravity——是否要应用地心引力
* m_ApplyFriction——空间触碰是否要应用摩擦力
这样,子类就可以自由选择要启用什么触碰测试元素。
看看如下来自Skeleton角色的片段:
package Code.Characters
{
import Code.Maths.Vector2;public class Skeleton extends Enemy
{
…/// <summary>
/// Apply collision detection only when not hurt
/// </summary>
public override function get m_HasWorldCollision( ):Boolean
{
return !IsHurt();
}/// <summary>
/// Apply gravity only when not hurt
/// </summary>
protected override function get m_ApplyGravity( ):Boolean
{
return !IsHurt();
}/// <summary>
/// Apply friction only when not hurt
/// </summary>
protected override function get m_ApplyFriction( ):Boolean
{
return !IsHurt();
}…
}
}
角色只是为了进行触碰测试,在未被“伤害”时,运用地心引力或摩擦力,这令角色能够在被玩家被杀死时呈现出和其他生物相同的样子。
物理原理
现在我们就来谈谈MoveableObject中的简单物理原理。各MoveableObject都具有特定位置、速度和半径。
半径来自Flash IDE——需在MoveableObject构造函数中检验实例物件,这必不可少,这样物理引擎就清楚物件的半径是多少。此半径就会变成半径X半径规格的AABB,因为触碰模型都是AABB结构。
位置是指物件在游戏空间中的方位(例如,像数),速度是像数/秒。MoveableObject的更新循环如下:
package Code.Physics
{
import flash.display.*;
import Code.Maths.Vector2;
import Code.*;
import Code.System.*;
import Code.Geometry.*;
import Code.Graphics.*;
import Code.Level.*;public class MoveableObject extends MovieClip implements IAABB, ICircle
{
…/// <summary>
/// Apply gravity, do collision and integrate position
/// </summary>
public function Update( dt:Number ):void
{
if ( m_ApplyGravity )
{
m_vel.AddYTo( Constants.kGravity );// clamp max speed
m_vel.m_y = Math.min( m_vel.m_y, Constants.kMaxSpeed*2 );
}if ( m_HasWorldCollision )
{
// do complex world collision
Collision( dt );
}// integrate position
m_pos.MulAddScalarTo( m_vel.Add(m_posCorrect), dt );// force the setter to act
m_Pos = m_pos;
m_posCorrect.Clear( );
}…
}
}
这部分有真正调用MoveableObject的各种功能,完全取决于我之前提到的子类性能执行方式。子类通过自己的Update()调用此功能,Update()有自己的逻辑。
这只是你的基本物理设置:
* 添加地心引力
* 进行触碰测试
* 结合位置
这基本就是当前游戏所需要的所有元素。
触碰测试
编写上述演示内容时,我进行众多有关平台游戏触碰测试技巧的调查,因为我知道,回到90年代这些游戏刚问世时,行业完全没有任何浮点单元和触碰测试研究,所以我相信其中定存在某些捷径,让我们能够轻松获得满意结果。
更新:我曾看到某篇关于SNES游戏《M.C.Kids》原始开发者如何基于触碰测试处理游戏图像方格的文章。
文章包含众多详细论述,但在执行方面,有些内容我不是很赞同;作者建议大家通过玩家周围的若干预定义点探测触碰情况,从而判断下步操作,具体如下:
作者这样写到:
若我们在顶部检查到的点处在稳固区域之中,我们会将玩家向下移动,这样顶点就会处在触碰区域的下方。若右侧点出现在稳固区域中,我们就会向左移动玩家,直到进攻点出现在碰触区域的左侧。通过六角形结构中的6个标点弹出玩家触碰的另一优点是,若玩家水平跳跃,脚碰到角落时,他将自动返回到平面上;若玩家向下偏向击中角落,或是脱离平台,他们将偏离墙面。
但我觉得,他最后提到的玩家自动触碰平面有些突兀,常常令我很好奇,玩家在体验游戏的过程中究竟发生了什么情况。我还发现,若玩家快速移动,然后进入某区域中时,这一策略无法发挥作用,因为所有点都处在区域中,我们无法找到解决问题的正确方式。而且,我发现自己需要的代码非常多,所以我决定放弃此策略——也许如果我的角色有像他所提到的那么高,情况会很多。
新方式和方格画面
显然,我需要新的方式,但首先先来谈谈方格画面坐标系及其如何将触碰测试变得简单而完善。
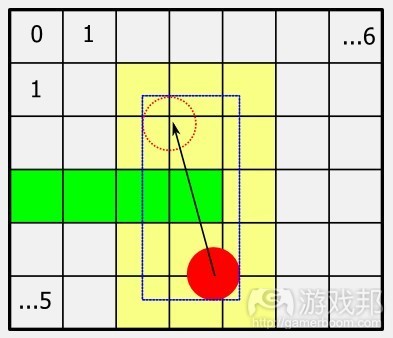
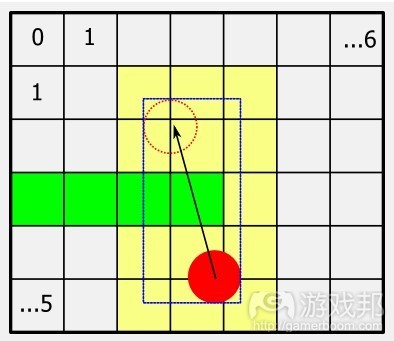
在图2中,方格画面坐标在X轴上标有0-6的数字,Y轴则是0-5。这呈现一个典型情境,玩家角色(以红色标记)向上跳跃,会在当前画面和下个画面之间击中绿色平台(玩家的速度以箭头表示)。要让触碰机制获悉哪个方格画面需要核对玩家位置,不妨融入玩家在坐标边界框或AABB中的运动范围。
图3以蓝色标记呈现情境的边界框。若我们突出所有同砖块画面交叉的边界框,我们就会清楚在玩家触碰测试方面,自己需要考虑哪个方格画面。
图4呈现的是以黄色标记的相关方格。
由于空间坐标和方格坐标间存在直接的1->1映像,我们能够轻松运用方格,然后进行相应的细颗粒触碰测试。这其实就是宽泛触碰测试机制所进行的操作,这是首先运用方格引擎所出现的直接结果,看起来非常赏心悦目。
新方式
若玩家移动过快,我们就不希望他们(游戏邦注:或其他快速移动的物件)穿越平台,因此细颗粒触碰检测机制需要足够完善,方能阻止这种情况发生。
我将运用我前面谈到的技巧Speculative Contacts。别担心虽然这听起来有些复杂,但其实相当简单。
这里需要的无非就是能够返回任何两个物体间距离的功能。
触碰模型
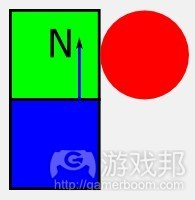
在我深入谈论细节前,我们有必要先来看看触碰模型的选择会如何影响游戏感觉。起初我以圆圈代表移动物件,但我很快发现这行不通。
原因很明显,详细请看图5;若放置得当,圆圈会流畅地从物件的边缘滑落下来,这是你在进行跳跃过程中所不希望发生的情况。
一个更好的选择是AABB结构,它不会旋转,因此能够让物件停止在平台边缘,就如图6所示。
距离函数
要在这里执行Speculative Contacts方式,我们需要能够传递两个AABB距离信息的距离函数。
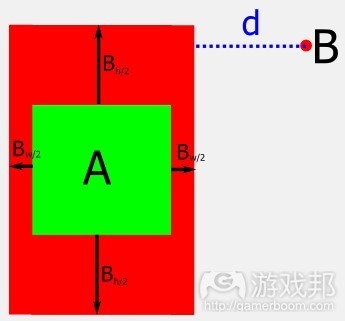
要做到这点,我们得转投源自Minkowski Difference的技巧。若我们将AABB缩成1个点,然后基于此AABB的规模扩展出另一AABB,问题就变成寻找此点和新AABB的距离。
图7:旨在找出AABB A和AABB B间的距离d。
图8:我们将B缩成1个点,以B的规模扩展A,然后我们就能够运用AABB到点函数的简单距离。
AABB到点的距离
我们其实只需要各坐标轴的最近距离,所以我们完全忽略AABB的角落是距离点的最近位置。
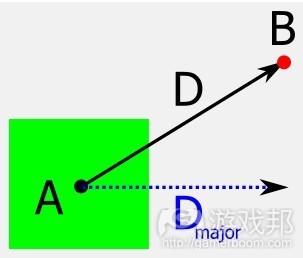
图9:要找到AABB A和点B的距离,我们要计算A->B, D的矢量,然后取矢量的Major Axis(长半轴)。也就是说,在标记的单位长度矢量中,填充其中的唯一坐标是原始矢量的最大坐标。
/// <summary>
/// Get the largest coordinate and return a signed, unit vector containing only that coordinate
/// </summary>
public function get m_MajorAxis( ):Vector2
{
if ( Math.abs( m_x )>Math.abs( m_y ) )
{
return new Vector2( Scalar.Sign(m_x), 0 );
}
else
{
return new Vector2( 0, Scalar.Sign(m_y) );
}
}
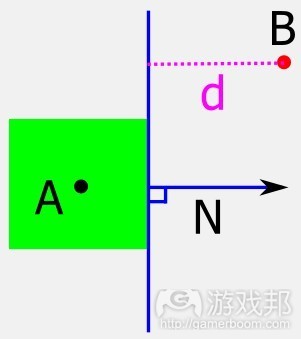
图10:Major Axis现在变成触碰的平面法向。通过将法向扩成A的一半尺寸及在空间中添加A的位置,我们得以计算出平面的位置。从点B到此新平面的距离d是点和AABB的最终距离,因此是两个AABB的距离。
Speculative Contacts
现在我们已把握所有运用此技巧所需的工具。
让我们再回到图4,现在我们要进行的就是查询地图,查看以黄色标识的方格是否能够进行触碰,若是如此,我们就需要像上面那样计算各点的距离和方向。
package Code.Physics
{
import flash.display.*;
import Code.Maths.Vector2;
import Code.*;
import Code.System.*;
import Code.Geometry.*;
import Code.Graphics.*;
import Code.Level.*;public class MoveableObject extends MovieClip implements IAABB, ICircle
{
…/// <summary>
/// Do collision detection and response for this object
/// </summary>
protected function Collision( dt:Number ):void
{
// where are we predicted to be next frame?
var predictedPos:Vector2 = Platformer.m_gTempVectorPool.AllocateClone( m_pos ).MulAddScalarTo( m_vel, dt );// find min/max
var min:Vector2 = m_pos.Min( predictedPos );
var max:Vector2 = m_pos.Max( predictedPos );// extend by radius
min.SubFrom( m_halfExtents );
max.AddTo( m_halfExtents );// extend a bit more – this helps when player is very close to boundary of one map cell
// but not intersecting the next one and is up a ladder
min.SubFrom( Constants.kExpand );
max.AddTo( Constants.kExpand );PreCollisionCode( );
m_map.DoActionToTilesWithinAabb( min, max, InnerCollide, dt );
PostCollisionCode( );
}/// <summary>
/// Inner collision response code
/// </summary>
protected function InnerCollide(tileAabb:AABB, tileType:int, dt:Number, i:int, j:int ):void
{
// is it collidable?
if ( Map.IsTileObstacle( tileType ) )
{
// standard collision responce
var collided:Boolean = Collide.AabbVsAabb( this, tileAabb, m_contact, i, j, m_map );
if ( collided )
{
CollisionResponse( m_contact.m_normal, m_contact.m_dist, dt );
}
}
else if ( Map.IsJumpThroughPlatform( tileType ) || Map.IsTileLadderTop(tileType) )
{
// these type of platforms are handled separately since you can jump through them
collided = Collide.AabbVsAabbTopPlane( this, tileAabb, m_contact );
if ( collided )
{
CollisionResponse( m_contact.m_normal, m_contact.m_dist, dt );
}
}
}…
}
}
上面片段呈现MoveabeObject类的相关代码。函数Collision是入口点。
package Code.Level
{
import Code.Geometry.AABB;
import Code.System.*;
import Code.Maths.Vector2;
import Code.*;public class Map
{
…/// <summary>
/// Call out to the action for each tile within the given world space bounds
/// </summary>
public function DoActionToTilesWithinAabb( min:Vector2, max:Vector2, action:Function, dt:Number ):void
{
// round down
var minI:int = WorldCoordsToTileX(min.m_x);
var minJ:int = WorldCoordsToTileY(min.m_y);// round up
var maxI:int = WorldCoordsToTileX(max.m_x+0.5);
var maxJ:int = WorldCoordsToTileY(max.m_y+0.5);for ( var i:int = minI; i<=maxI; i++ )
{
for ( var j:int = minJ; j<=maxJ; j++ )
{
// generate aabb for this tile
FillInTileAabb( i, j, m_aabbTemp );// call on the mid-ground map (ladders and special objects)
action( m_aabbTemp, GetMidgroundTile( i, j ), dt, i, j );
}
}for ( i = minI; i<=maxI; i++ )
{
for ( j = minJ; j<=maxJ; j++ )
{
// generate aabb for this tile
FillInTileAabb( i, j, m_aabbTemp );// call the delegate on the main collision map
action( m_aabbTemp, GetTile( i, j ), dt, i, j );
}
}
}…
}
}
上述片段呈现我在图4地图方格中进行循环操作所涉及的代码。你会发现我进行两次循环,1次针对中间方格,1次针对近景位置。这主要是因为梯子目前影射在中间图层。未来我想要尝试在近景位置单独绘制这些内容,虽然这会让代码变小。
Speculative Contacts的有趣之处在于,它在非必要时候就不会进行运作——所以,通过图4的所有黄色方格,我们能够算出当时各点的位置和法向,但函数CollisionResponse就不会进行任何操作,除非下述条件成立:
var nv:Number = m_vel.Dot( normal ) + separation/dt;
if (nv < 0)
{
// do something
}
这里的意思是:若物件到接触法向的映射速度小于两个物件的最近距离(游戏邦注:除以时间步就能够转化成相同单位),那就不要进行任何操作。若物件无法在此画面和下个画面间接触,那就不执行任何操作。
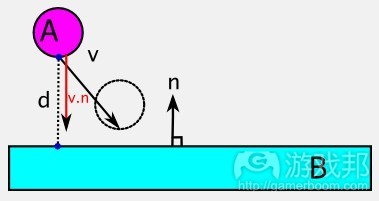
图11在图表格式中就呈现这点,当A朝B靠拢时,若映射速度(v.n)小于物件间的距离d,那么触碰就具有可能性。
这里没有什么注意事项,因为若物件的移动速度够快,幽灵触碰就具有可能性。出现这种情况是因为CollisionResponse代码只知道触碰点的广泛平面,而不清楚实际几何结构,所以快速移动的物件有时就会击中靠近物件表面的真空区,而不是从此穿过。但这不是游戏中的抢眼道具,主要因为所有物件的最大速度都遭到限制。
内部边界
许多触碰检测机制所存在的主要问题都是内部边界,遗憾的是,这款游戏也不例外。
在图12中,红球将用于判定蓝色区域的触碰操作,距离函数会呈现单位矢量N,作为最靠近的方向,这单独来看没有什么问题,但由于两边都有其他区域,以及这其实是个连续平面,问题就随之产生。若我们没有采取措施阻止这种情况,玩家就会卡在区域的间隙中,甚至还要能够在垂直区域的间隙站立。
解决方案
为阻止这种情况的出现,我在触碰测试机制中放置若干特殊代码,这能够检测内部边界。
package Code.Geometry
{
import Code.System.*;
import Code.Maths.*;
import Code.Geometry.*;
import Code.Characters.Character;
import Code.Level.*;
import Code.eTileTypes;
import Code.Platformer;
import Code.Constants;public class Collide
{
/// <summary>
/// Helper function which checks for internal edges
/// </summary>
static private function IsInternalCollision( tileI:int, tileJ:int, normal:Vector2, map:Map ):Boolean
{
var nextTileI:int = tileI+normal.m_x;
var nextTileJ:int = tileJ+normal.m_y;var currentTile:uint = map.GetTile( tileI, tileJ );
var nextTile:uint = map.GetTile( nextTileI, nextTileJ );var internalEdge:Boolean = Map.IsTileObstacle(nextTile);
return internalEdge;
}…
}
}
这仅仅是为了检查地图,看看其当前方块的相邻位置是否存在另一可触碰方格。这里的“相邻位置”是指某方格沿着当前方格的触碰法向。若存在阻碍方格,此触碰就会被标记成内部边界,机制就会将此放弃。
回到图12,我们检验的区域是法向指向的位置,这是个可触碰区域,所以触碰就消失。
穿过平台
有些类型的平台游戏是由稳固的平台构成,玩家无法穿越这些平台,但《Newzealand Story》和《Rainbow Islands》所包含的平台,就允许玩家穿越。
为让游戏引擎保持较高灵活性,我打算融入两种模式。
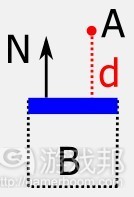
要做到这点,我就需要能够呈现点与另一点顶部平面距离的距离函数(游戏邦注:记住我们将AABB缩成一个点,然后扩展另一AABB)。即便如此,我就只是想要着眼于它们间的触碰,假设移动物件足够接近AABB的顶部平面——若情况不是如此,那么触碰就会消失。
图14呈现的是玩家穿越平台B和移动物件A,这是玩家同B顶部平面的距离d,N是长半轴(major axis)。
除常规AABB & AABB代码外,这里还有两个触碰接受条件。
* 长半轴的方向向上,例如这是个地面平台
* 移动物件同平台顶部的距离大于负公差
若这些条件满足,那么触碰就能够形成。若没有,就会遭到拒绝。负公差呈现的是平台下与平台上的过渡情况。其为负值的原因是若移动物件在平台之下,距离就是负数;随着物件向上移动,直至处在平台上的0值,其负值趋势会逐步减弱,最终会变成正值。此公差就是图14中的蓝色横条。
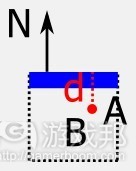
图15呈现的是拒绝情况,其中移动物件处在公差蓝色横条的极下方。
触碰回应
这里运行的触碰回应只是为了在触碰时完全移除移动物件的法向速度。这意味着物件不会弹跳,但在这款游戏中,这是能够接受的让步情况。
package Code.Physics
{
import flash.display.*;
import Code.Maths.Vector2;
import Code.*;
import Code.System.*;
import Code.Geometry.*;
import Code.Graphics.*;
import Code.Level.*;public class MoveableObject extends MovieClip implements IAABB, ICircle
{
…/// <summary>
/// Collision Reponse – remove normal velocity
/// </summary>
protected function CollisionResponse( normal:Vector2, dist:Number, dt:Number ):void
{
// get the separation and penetration separately, this is to stop pentration
// from causing the objects to ping apart
var separation:Number = Math.max( dist, 0 );
var penetration:Number = Math.min( dist, 0 );// compute relative normal velocity require to be object to an exact stop at the surface
var nv:Number = m_vel.Dot( normal ) + separation/dt;// accumulate the penetration correction, this is applied in Update() and ensures
// we don’t add any energy to the system
m_posCorrect.SubFrom( normal.MulScalar( penetration/dt ) );if ( nv<0 )
{
// remove normal velocity
m_vel.SubFrom( normal.MulScalar( nv ) );// is this some ground?
if ( normal.m_y<0 )
{
m_onGround = true;// friction
if ( m_ApplyFriction )
{
// get the tanget from the normal (perp vector)
var tangent:Vector2 = normal.m_Perp;// compute the tangential velocity, scale by friction
var tv:Number = m_vel.Dot( tangent )*kGroundFriction;// subtract that from the main velocity
m_vel.SubFrom( tangent.MulScalar( tv ) );
}if (!m_onGroundLast)
{
// this transition occurs when this object ‘lands’ on the ground
LandingTransition( );
}
}
}
}…
}
}
头几行主要是运算间隔和渗透(物件距离的积极或消极元素)。
// get the separation and penetration separately, this is to stop pentration
// from causing the objects to ping apart
var separation:Number = Math.max( dist, 0 );
var penetration:Number = Math.min( dist, 0 );
然后,我计算相对法向速度,收集处理渗透分辨率的位置修正矢量:
// compute relative normal velocity require to be object to an exact stop at the surface
var nv:Number = m_vel.Dot( normal ) + separation/dt;// accumulate the penetration correction, this is applied in Update() and ensures
// we don’t add any energy to the system
m_posCorrect.SubFrom( normal.MulScalar( penetration/dt ) );
若法向速度低于0,例如,物件会在此画面和下个画面间进行触碰,游戏就会移除移动物件的法向速度:
if ( nv<0 )
{
// remove normal velocity
m_vel.SubFrom( normal.MulScalar( nv ) );
若这是我将进行触碰的地面,记录实际情况,然后如果我们需要运用摩擦力,不妨这么做:
m_onGround = true;
// friction
if ( m_ApplyFriction )
{
// get the tanget from the normal (perp vector)
var tangent:Vector2 = normal.m_Perp;// compute the tangential velocity, scale by friction
var tv:Number = m_vel.Dot( tangent )*kGroundFriction;// subtract that from the main velocity
m_vel.SubFrom( tangent.MulScalar( tv ) );
}
若在上个触碰中,我们未被记录为位于平面上,那么就调用处理地面降落的代码(这是用户可定义代码):
if (!m_onGroundLast)
{
// this transition occurs when this object ‘lands’ on the ground
LandingTransition( );
}
就是这样!唯一令人棘手的地方是摩擦触碰,但依然算是相对简单——只是让单位长度的矢量垂直于法向(例如,滑动矢量),计算物件在滑动方向的速度,根据摩擦系数进行收缩,然后将此从总速度中扣除。
图13呈现的是切向速度的运算;若你打算将此切向速度从完整速度中移除,将会遇到较多摩擦。
若你想要了解触碰回应代码的更多细节内容,我建议你阅读《Physics Engines For Dummies》。(本文为游戏邦/gamerboom.com编译,拒绝任何不保留版权的转载,如需转载请联系:游戏邦)
How to make a 2d platform game – part 2 collision detection
By Paul
In this series of articles, I’m talking about the technology behind a platform game.
If you missed part 1 you can check it out here.
The language is actionscript 3.0, but the techniques are applicable to all languages.
In this particular article I’m going to talk about the physics, collision detection and AI aspects of the game.
There is a playable version at the bottom of the post, for those with Flash support in browser.
Class hierarchy
It makes sense at this point to talk about the class hierarchy I’ve used in the game, to represent everything which moves:
Figure 1 shows the class hierarchy – at the very top sits MoveableObject, which is where all the generic collision detection and response gets done; I say generic because the player does specialised work to handle things like ladders etc.
Each level in the hierarchy represents separate functionality; for example, Character contains the AnimationController which handles playing the various different animations for each character, SimpleEnemy represents a certain class of enemy character which does no collision detection with the world, and obeys special position markers when it encounters them. The Diamond pickup is a simple object which has no AI, and just collides with the world, so it inherits from the base class, since that’s all the functionality it needs.
This may seem like a lot of extra complexity for such a simple game, but it really makes adding new enemy types very easy indeed, and simplifies the debugging process because there is so much code shared between each object.
If I had to give one piece of advice from 10 years of game development it would be this: avoid code duplication at all costs. It leads to slow development and bug city whereby you fix a bug in one location, and then forget to fix it in the other duplicated locations.
MoveableObject has certain properties which it requires be implemented by any class which inherits from it:
* m_HasWorldCollision – whether full collision detection should be performed
* m_ApplyGravity – whether gravity should be applied
* m_ApplyFriction – whether the world collision should apply friction
That way, and child class can chose what elements of collision detection it wants enabled.
Consider the following snippet from the Skeleton character:
Its been set up to only do collision detection, apply gravity or friction when its not been ‘hurt’ (i.e punched by the player), this allows it to have the same behaviour as all other creatures when the player kills them.
Physics
Ok, so lets talk about the simple physics inside MoveableObject. Every MoveableObject has a position, a velocity and a radius.
This radius comes from the Flash IDE – an object instance called ‘m_flaCollision’ is checked for in the constructor of MoveableObject, and is a requirement, so the physics engine knows what the object’s radius is. This radius is then turned into an AABB of size radius x radius, because the collision shapes are all AABBs.
Position is the position of the object in world space (i.e. pixels) and velocity is pixels/second. The update loop for MoveableObject looks like this:
This is the part which actually calls out to the various features of MoveableObject and depends on the child class’s implementation of those properties I discussed earlier. Child classes call out to this function from their own Update() which contains their specific logic.
This is just your basic physics set-up:
* Add gravity
* Do collision detection
* Integrate position
This is basically all we need for the game as it stands.
Collision detection
When writing the demo above, I did a lot of research on collision detection techniques for platform games because I knew that back in the 1980s when these games first came out, there were no floating point units and collision detection research was in its infancy, so there must be some really easy tricks you can do to get a great result nice and simply.
Update: I wish I’d found this article before I started writing this, its about how the original developers of M.C.Kids on the SNES handled tile based collision detection. In summary its kind of similar to the article I reference below, in that it used collision points, only it goes into more detail about all the ins and outs of the technique.
This article contains the most detailed explanation that I could find, but on implementing it I found there were a few things I didn’t like; the author advocates using a number of predefined points around the player to help detect collisions and to judge what to do next, like this:
The author writes:
If the point we check on top goes inside a solid block, we move the player downward so that the top point is just below the block it bumped into. If either right point goes inside a solid block, we move the player left until the offending point is just left of the block it bumped into, and so on…
Another benefit of detecting player collision using six points in that hexagon configuration is that if the player is jumping horizontally and the feet hit a corner, the player is automatically bumped up onto the surface; if the player falling vertically hits a corner off-center, or steps off a ledge, the player slides off away from the wall. (Try this! It feels much better than it would if the player behaved as a boxy rectangle.)
However, I found that the last part he mentions about the player being automatically bumped onto the surface was very jarring and often left me wondering what had happened while playing the game. I also found that it didn’t help me when the player was moving quickly and became embedded inside a block, because with all points inside the block, there was no clearly correct way to resolve. Also, the amount of code I found I needed was getting excessive so I decided to discard this method – maybe it would have been better if my player character was taller like in his example.
A new way and tiles as a broad-phase
Obviously I needed a new way, but first lets talk about the tile coordinate system and how it makes collision detection nice and easy.
Consider Figure 2 in which the tile coordinates have been numbered 0-6 in the X axis, and 0-5 in the Y. This shows a typical scenario where the player character (shown in red) is jumping up and will hit the green platform at some point between the current frame and the next frame (the player’s velocity is shown as the arrow). In order for the collision system to know which tiles need checking against the player, its a simple matter to enclose the player’s range of motion within an axis aligned bounding box, or AABB.
Figure 3 shows this bounding box overlaid on the scene in blue. If we take that bounding box and highlight every tile which intersects with it, we now know which tiles we need to consider for collision detection against the player.
Figure 4 shows the relevant tiles highlighted in yellow.
Because there is a direct 1->1 mapping between world coordinates and tile coordinates, it becomes incredibly easy to get access to the tiles in order to perform fine grained collision detection against. This is in essence what a broad-phase collision detection system does, and its refreshing to see it arise naturally as a direct consequence of using a tile engine in the first place.
The new way
Because we don’t want the player (or any other fast moving object) passing though platforms if they move too quickly, the fine grained collision detection system, or narrow phase, must be good enough to prevent this from happening.
I’m going to use a technique I first talked about a while back, called Speculative Contacts. Don’t worry if it sounds horribily complex, its actually rather simple.
All it requires to work is a function which can return the distance between any two objects.
The collision shape
Before I go into the details, its important that I talk about how the choice of collision shape will affect the feel of the game. I started out with a circle to represent moving objects, but I soon realised this wasn’t going to work.
The reason is obvious looking at Figure 5; circles tend to roll smoothly off the edges of objects when placed right on them, which is exactly what you don’t want happening when you’re lining yourself up for a jump.
A better choice is the AABB, which naturally cannot rotate and therefore will allow objects to perch right on the edge of platforms without falling off them, as shown in Figure 6.
Distance function
In order to implement Speculative Contacts in this case, we need a distance function which will give us distance between two AABBs.
In order to achieve this we turn to the a technique from the Minkowski Difference. If we shrink one AABB down to a point, and grow the other one by the extents (width and height) of the first, the problem becomes one of finding the distance between the point and the new AABB.
Figure 7: In order to find the distance d, between AABBs A and B…
Figure 8: We shrink B down to a point and expand A by the extents of B, then we can use a simple distance from AABB to point function.
Distance from AABB to point
We actually only need the closest distance in each axis for our purposes, so we’re ignoring the case where the corner of the AABB is the closest to the point.
Figure 9: To find the distance between AABB A and point B we calculate the vector from A->B, D and then take the Major Axis of this vector. That is, the signed, unit length vector in which the only coordinate filled in represents the largest coordinate of the original vector.
Figure 10: The Major Axis has now become the plane normal for our collision. We can calculate the position of the plane by scaling this normal by the half extents of A and adding on the position of A in world space). The distance d, from point B to this new plane is the final distance between point and AABB, and thus the distance between two AABBs.
Speculative Contacts
Now we have all the tools we need to get this technique working!
Looking back at Figure 4 again, all we have to do now is to query the map to see if any of those tiles highlighted in yellow are collidable and if so, we must calculate the distance to each one and the normal as we did above.
The above snippet shows the relevant code in the MoveabeObject class. The function Collision is the entry point.
The above snippet shows the code which actually does the looping over the tiles in the map shown in Figure 4. You can see that I do two loops, one for the mid-ground tiles and one for the foreground. This is primarily because of ladders which are currently mapped in the mid-ground layer. I would like to explore mapping them solely in foreground in a future version, though as it would make the code smaller.
The interesting thing about Speculative Contacts is that they do no work if they’re not required to – so, for all the yellow tiles in Figure 4 we calculate the distance to each one and the normal at that point, but the function CollisionResponse doesn’t do anything unless the following condition is true:
What this is saying is: if the projection of the velocity of the object onto the contact normal (i.e. the velocity in the normal direction) is less than the closest distance between the objects (divided by the timestep, to convert to the same units), then do nothing. I.e. if the objects can not touch between this frame and next, do nothing.
Figure 11 show this in diagram form, A is heading towards B and the projected velocity is shown (v.n) but is shorter than the distance between objects d and so no collision is possible.
There is one important caveat to mention, in that if the objects are moving fast enough, ghost collisions are possible – whereby one object will appear to hit an object that it shouldn’t have. This occurs because the CollisionResponse code only knows about the infinite plane of the collision point and not the actual geometry (for performance reasons), so a fast moving object will sometimes hit the empty space next to the surface of the object rather than passing through. However, this is not a noticeable artefact in the game shown on this page, particularly because the maximum speed of all objects is clamped.
Internal edges
One of the problems that a lot of collision detection systems face is that of internal edges and unfortunately, this game is no different.
In Figure 12, the red ball will be judged for collision against the blue block, and the distance function will return the unit vector N as the closest direction, this is correct in isolation, but considering there are other blocks on either side and this is in fact one continuous surface, problems arise. If nothing is done to prevent this, the player will get stuck on the gap between blocks and will even be able to stand the gaps between vertical blocks.
Solution
To prevent this from happening, I have some special code in the collision detection system which checks for internal edges.
What this does is to simply check the map to see if there is another collide-able tile ‘next to’ the current one. ‘Next to’ is defined as one tile along from the current one in the direction of the collision normal. If there is a tile there which is an obstacle, this collision is marked as an internal edge and the system discards it.
Going back to Figure 12, the block which is checked is the one pointed to by the normal, this is a collide-able block and so the collision is discarded correctly.
Jump-through platforms
Some types of platform game are built of completely solid platforms which you cannot jump through, but others like The Newzealand Story and Rainbow Islands are built entirely of platforms that the player can jump through.
To make this game engine as flexible as possible I wanted to support both.
In order to achieve this I needed a distance function which would give me the distance between an point and just the top plane of another (remember we shrunk down one AABB to a point and grew the other). Even still, I only want to consider colliding with this if the moving object was sufficiently close to the top plane of the AABB – if not, the collision is discarded.
Figure 14 shows jump-through platform B and movable object A, which is d distance to the top plane of B and N is the major axis.
There are two collision acceptance conditions on top of the regular AABB vs AABB code.
* If the major axis is pointing up, i.e. this is a ground platform
* If the distance of the moving object to the top of the platform is greater than some negative tolerance
If these conditions are satisfied then the collision is accepted. If not, its rejected. The negative tolerance is to handle the transition between being just under the top of the platform and being on it. Its negative because when the moving object is below the platform, the distance is always negative; it grows less and less negative as the object moves up until its 0 right on the platform, then it becomes positive again. This tolerance is shown as the blue bar in Figure 14.
Figure 15 shows one discarded case, where the moving object is too far below the blue bar of tolerance.
Collision Response
The collision response at work here is just to remove the normal velocity of the moving object completely upon collision (and also correct for any penetration which occurs). This means objects do not bounce, but for this game, that is an acceptable compromise.
The first few lines compute the separation and penetration (positive or negative components of the distance between objects)
Then, I compute the relative normal velocity and accumulate the position correction vector which handles penetration resolution:
If the normal velocity is less than 0, i.e the objects will touch between this frame and next, remove the normal velocity from the moving object:
If this is a piece of ground we’re going to collide with, record that fact, and then if we need to apply friction, do so:
If we weren’t recorded as being on the ground in the last collision, then call out to some code which handles landing on the ground (this is user definable code):
And that’s it! The only slightly hairy part is the friction calculation, but even that is relatively simple – it just gets the unit length vector perpendicular to the normal (i.e. the sliding vector), calculates the object’s velocity in the sliding direction, scales that down by some friction coefficient and then subtracts that from the total velocity.
Figure 13 shows the computation of the tangential velocity; if you were to remove this tangential velocity from the full velocity you would have infinite friction.
If you would like more in-depth details of the collision response code, I suggest you read Physics Engines For Dummies, which covers this in great detail.
End of part 2
Wow, I thought I would have space to talk about the AI in this article, but obviously not! There was an unexpectedly large amount of collision detection to discuss. Ok, so next time I will definitely talk more about the AI and the software engineering behind it all.
As ever, if you want, you can buy the source-code for the entire game (or even try a version for free), including all the assets and levels you see above. It will require Adobe Flash CS4+, the Adobe Flex Compiler 4.0+ and either Amethyst, or Flash Develop to get it to build. And you’ll want Mappy or some alternative in order to create your own levels!
Following on from feedback from the Angry Birds article, I’ve included a Flash Develop project as well as an Amethyst project inside the .zip file, to help you get started more quickly, no matter which development environment you have.
You are free to use it for whatever purposes you see fit, even for commercial games or in multiple projects, the only thing I ask is that you don’t spread/redistribute the source-code around. Please note that you will need some programming and design skills in order to make the best use of this!(Source:wildbunny)












































 闽公网安备35020302001549号
闽公网安备35020302001549号